ENGR 21 Fall 2025

HW 7

• HW 7
  • Summary
  • Some Tips
  • (1) Gaussian Elimination in Python
    • (1.1) Forward Elimination
    • (1.2) Backward Substitution
  • (2) Gaussian Elimination by hand
  • (3) The condition number.
  • (4) Using linear systems to solve circuits

Summary

Due Date: Tue, Oct 28 at midnight
What to submit:

• A PDF file that contains
  • the completed template from problem 2
  • the answers to problem 3.
  • the system of equations for problem 4
• GaussianElimination.py from problem 1
• The code that you used to solve problem 4. Where to submit:
• Code at this link
• PDF at this link

Some Tips

Built-in methods to solve linear systems

numpy already contains the capabilities to solve linear systems efficiently. If a solution to a linear system Ax=b exists, numpy can find it using built-in methods.

For example, the following code works:

from numpy import dot
from numpy.linalg import inv as invert

# Assuming A is a square matrix and b is a column vector:
x = dot(invert(A),b)

Calculating the norm

numpy can calculate the norm. Just include the line

from numpy.linalg import norm

and then use the function norm.

(1) Gaussian Elimination in Python

In this problem, you will write a program that solves a linear system of equations using Gaussian elimination followed by forward substitution. Turn in both functions that you write in a single python file called GaussianElimination.py.

(1.1) Forward Elimination

Write a function named forward_elimination that takes as input a matrix A and a column vector b. It should output the augmented matrix after it has been put in ‘row echelon form’, i.e., after the lower-left portion has been appropriately replaced with zeros. Note that:

• your function should work with numpy arrays.
• b must be a column vector in numpy. See below for an example of how to create a column vector using numpy.
• Your program should return None if there are any size discrepancies. You should think about the possible ways in which the size of A or b may be incompataible with the Gaussian elimination procedure.

Hint: You may find it helpful to use the function numpy.concatenate((A,b),axis=1).

import numpy as np
def forward_elimination(A,b):
    # A is a square matrix of size N x N,
    # e.g., [[1,2,3],[1,4,5],[0,1,2]]
    # b is a column vector of size N x 1
    # e.g., [[-1],[5],[7]]
    # Function returns augmented matrix [A | b]
    
    aug = np.concatenate((A,b),axis=1)
    return aug

Try out your code on the problem that was on the slides for Tuesday’s lecture, i.e., when you provide the following variables to your function:

A1 = np.array([[2,1,-1,2],
               [4,5,-3,6],
               [-2,5,-2,6],
               [4,11,-4,8]])

b1 = np.array([[5],
               [9],
               [4],
               [2]])

and then call your function on it, the result should be as shown below.

>>> forward_elimination(A1,b1)

[[ 2  1 -1  2  5]
 [ 0  3 -1  2 -1]
 [ 0  0 -1  4 11]
 [ 0  0  0  2  6]]

(1.2) Backward Substitution

Write a Python function that performs backward substitution. The function should take as input an ‘augmented matrix’, and should output a column vector of values corresponding to the solution to the system of equations $Ax=b$.

Hint: Recall that A[:,-1] returns the last column of a matrix.

import numpy as np
def backward_substitution(Ab):
    # Input is a N x (N+1) matrix
    # output is a column vector of size N x 1

    # Initialize your 'x' vector that will contain your solution
    x = np.zeros((N,1))

    return x

(2) Gaussian Elimination by hand

Fill in the following template to carry out Gaussian elimination by hand on the following matrix $A$ and right-hand-side $b$:

\[A =\begin{bmatrix} 2 & 1 & -1 & 0\\ 1 & 1 & 2 & 0\\ -1 & 2 & 1 & 1\\ 6 & 1 & 1 & -2 \end{bmatrix}, \quad b = \begin{bmatrix} 1 \\ -1 \\ 0 \\ 2 \end{bmatrix},\]

(###) Template

(3) The condition number.

Consider the matrix \(\begin{bmatrix} 4.1 & 2.8 \\ 9.7 & 6.6 \end{bmatrix},\) and the right-hand side vector \(\begin{bmatrix} 4.1 \\ 9.7 \end{bmatrix}.\)

Use any method to calculate the solution to the equation $Ax=b$ where $A$ is the matrix above and $b$ is the right-hand side vector above. What is the solution?

Repeat the above question, but this time using \(b = \begin{bmatrix} 4.11 \\ 9.7 \end{bmatrix}.\) What is the solution $x$ ?

Comment on how this behavior is related to the condition number.

(4) Using linear systems to solve circuits

The ammeter readings in the following circuit can be considered to be the solution to a linear system of equations. Write out this system of equations by hand using Kirchhoff’s Laws, and then use your Gaussian elimination and backward substitution programs to verify the four ammeter redings shown in the following circuit diagram.

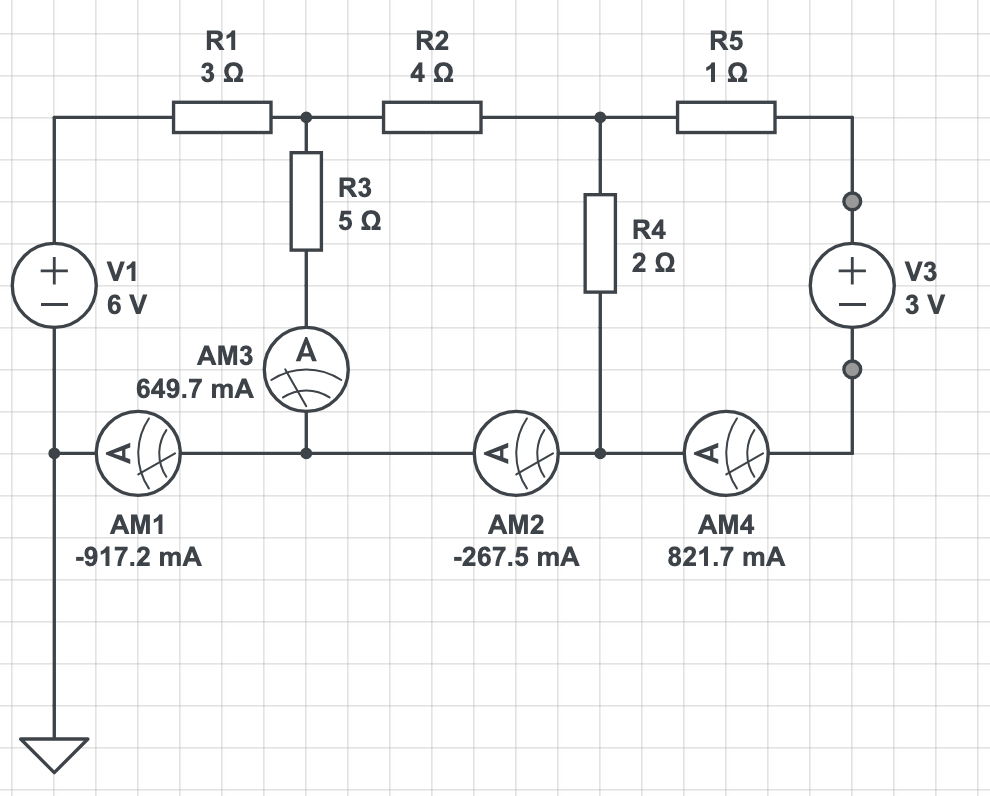
Turn in your code, including appropriate print statements so that the graders can verify your work.