ENGR 21 Fall 2025

Resources

External Guides and Tutorials

If Mu does not work for you on Windows, you can follow these instructions to use PuTTY as your console as an alernative.

Instructor’s Circuit Playground Guide for E21

To use any of these features, make sure your Python code includes the following line at the top:

Taps and shakes

cp.shake()  # Returns True if it's currently being shaken
cp.shake(shake_threshold=20)  # optional parameter to change sensitivity

cp.tapped # Returns True if it's currently being tapped
cp.detect_taps  # A variable that can be set to either 1 or 2; 2 looks for double taps.

Switching on the Red LED

cp.red_led = True  # switches on the red LED

Detecting state of Slide switch

cp.switch  # returns True or False

Using the Neopixels

There are 10 neopixels. The state of each is determined by a 3-tuple of RGB values, i.e. (p,q,r) where each element of the tuple is an integer between 0 and 255 and represents the red, green and blue channels respectively.

The full state of the neopixels is determined by a 10-element list of 3-tuples, i.e., 30 numbers in total, arranged in the form

[(0, 0, 0), (0, 0, 0), (0, 0, 0), (0, 0, 0), (0, 0, 0), (0, 0, 0), (0, 0, 0), (0, 0, 0), (0, 0, 0), (0, 0, 0)]

the variable cp.pixels contains the above list.

You can set individual elements of the neopixels, e.g., turn the 4th pixel to a mild green like so:

cp.pixels[4] = (0,10,0)  # for pixel number 4, set red to 0, green to 10, and blue to 0

There is also a convenient method, cp.pixels.fill(), which you can use to control all the pixels at the same time. You must pass a 3-tuple to this method.

cp.pixels.fill((10,0,0))  # set red channel to a strength of 10 for all the neopixels.

Reading the light sensor

The light sensor on the Circuit Playground Bluefruit detects ambient light and returns an integer between 0 and ?. Access the curent reading of the light sensor using

cp.light

Reading raw data from the accelerometer

Access the raw data from the accelerometer in meters per seconds squared using

cp.acceleration

This yields an object of class acceleration with three attributes: x, y, and z. Thus,

cp.acceleration.z

returns the acceleration in the z direction.

Physical buttons A and B

There are two buttons on the Circuit Playground Bluefruit, labeled A and B. The boolean variables

cp.button_a
cp.button_b

are True while the corresponding buttons are pressed.

Temperature sensor

The temperature sensor on the Circuit Playground Bluefruit detects ambient temperature and returns a real number equal to the temperature in Celsius. Access the current temperature in Celsius using

cp.temperature

Capacitive Touch

Seven of the pins on the Circuit Playground Bluefruit can take capacitive touch input. image

These are A1, A2, A3, A4, A5, A6, and TX. You can see these names on the capacative input regions on the edges of the board, i.e. the mounting holes. The variable cp.touch_A1 will be True when pin A1 is being touched, and will be False otherwise. Thus, there are seven such variables:

Speaker

Lec 1.1, Tue Sep 2

Installation Instructions

  1. Installing Circuit Python on your Circuit Playground Bluefruit. This will install Circuit Python, a compact and pared-down version of Python for embedded systems.
  2. Installing Mu on your computer. This is the IDE that we will use for Circuit Playground.
  3. Downloading Libraries and copying them on to Circuit Playground Bluefruit. Make sure you use the libraries from Circuit Python 9! Note that you must copy 2 folders and 3 files into the lib folder of your Circuit Playground device.

Sample First Code to run on your board

from adafruit_circuitplayground import cp

while True:
    cp.pixels[4] = (10,0,10)
    if cp.button_a:
         cp.play_tone(440,1)
    if cp.button_b:
         cp.play_tone(220,1)

Lec 2.1, Tue Sep 9

from adafruit_circuitplayground import cp
import time

for j in range(200):
    print("Pin A1 digital read:",cp.touch_A1)
    print((int(cp.touch_A1),))
    if cp.touch_A1:
        cp.pixels[3] = (0,25,0)
    else:
        cp.pixels[3] = (25,0,0)
    time.sleep(0.1)

import board
import analogio
import time

pin_a1 = analogio.AnalogIn(board.A1)

for j in range(200):
    print("Pin A1 analog read:",pin_a1.value)
    print((pin_a1.value,))
    time.sleep(0.1)


import board
import analogio
import time
import neopixel

pin_a1 = analogio.AnalogIn(board.A1)
pixels = neopixel.NeoPixel(board.NEOPIXEL, 10, auto_write=False)

for j in range(200):
    print("Pin A1 analog read:",pin_a1.value)
    print((pin_a1.value,))
    mapped_brightness = 150 # change this!
    pixels[3] = (0,mapped_brightness,0)
    pixels.show()
    time.sleep(0.1)

Lec 2.2, Thu Sep 11

(0) Code for Truth Table

# Set the values of A and B
A = True
B = False

# Implement “Logic gate OR” by covering all four possibilities.

if A == True:
    if B == True:
        C = True # line 1 of table
    else:
        C = True # line 2 of table
else:
    if B == True:
        C = True # line 3 of table
    else:
        C = False # line 4 of table

print("--After applying logic, C is",C)

(1) Code for time package

from adafruit_circuitplayground import cp

import time

delay = 3.0

print("Switching on pixel 0")
cp.pixels[0] = (0,10,0)
print(f"Waiting for {delay} seconds")
time.sleep(delay)

print("Switching on pixel 1")
cp.pixels[1] = (10,0,0)
print(f"Waiting for {delay} seconds")
time.sleep(delay)

print("Switching on pixel 2")
cp.pixels[2] = (0,0,10)
print(f"Waiting for {delay} seconds")
time.sleep(delay)

(2) Code for print statements

print(“The number is 24”)

p = 24.1
n = 24

print(“The numbers are n and p”)

print(“The numbers are {n} and {p}”)

print(f“The numbers are {n} and {p}”)

print(f"The numbers are {n:} {p:.3f}")

c = "The numbers are {} and {}".format(p,n)
print(c)

(3) Code for for loops

# Iterable (1): Range
print("Printing fron a range:")
for j in range(2,10,2):
    print(j)

# Iterable (2): list
print("Printing fron a list:")
a = [1,"a",6,"hello",5,True]
for j in a:
    print(j)

# Iterable (3): tuple
print("Printing fron a tuple:")
b = (1,2,"x",3,1)
for k in b:
    print(k)

# Iterable (4): string
print("Printing characters from a string:")
c = "hello"
for x in c:
    print(x)

(4) The break keyword

# break inside for loop
for j in range(10):
    print(j)
    if j == 3:
        print("exiting loop")
        break

# break inside while loop
counter_variable = 0
while 3 > 2:
    counter_variable += 1
    if counter_variable > 3:
        break

(5) The continue keyword


# break inside for loop
for j in range(10):
    print(j)
    if j == 3:
        print("exiting loop")
        break

# break inside while loop
counter_variable = 0
while 3 > 2:
    counter_variable += 1
    if counter_variable > 3:
        break

(6) Light up neopixels

from adafruit_circuitplayground import cp
import time

cp.pixels[0] = (10,10,10)
time.sleep(1)
cp.pixels.fill((0,0,0))

cp.pixels[1] = (30,30,30)
time.sleep(1)
cp.pixels.fill((0,0,0))

cp.pixels[2] = (50,50,50)
time.sleep(1)
cp.pixels.fill((0,0,0))

cp.pixels[3] = (70,70,70)
time.sleep(1)
cp.pixels.fill((0,0,0))

Lec 3.1, Tue Sep 16

Accelerometer Code

from adafruit_circuitplayground import cp
import time

def std(data):
    mean = sum(data) / len(data)
    squared_diffs = [(x - mean) ** 2 for x in data]
    variance = sum(squared_diffs) / len(data)
    std_dev = variance ** 0.5
    return std_dev

def magnitude(a,b,c):
    return (a**2 + b**2 + c**2)**(1/2)

# Number of readings
N = 10

# Create a list that will store the readings
readings_z = [0] * N
readings = [0] * N

# Time delay between measurements
delay = 2

for j in range(N): # Number of seconds to run
    accel_z = cp.acceleration.z
    accel   = magnitude(cp.acceleration.x, cp.acceleration.y,cp.acceleration.z)
    print((accel_z,accel))
    readings[j] = accel
    readings_z[j] = accel_z
    time.sleep(delay) # delay of 1 second

avg_reading = sum(readings)/len(readings)
avg_reading_z = sum(readings_z)/len(readings_z)
print("After ",N," readings, the acceleration is ",avg_reading," m/s^2")
print("With standard deviation ",std(readings))
print("After ",N," readings, the z-acceleration is ",avg_reading_z," m/s^2")
print("With standard deviation ",std(readings_z))

Writing data to Circuit Playground Bluefruit

Copy the file boot.py into your CIRCUITPY drive. The contents of this file are shown below for reference.

"""CircuitPython Essentials Storage logging boot.py file adapted from Adafruit"""
import board
import digitalio
import storage

# For Circuit Playground Express, Circuit Playground Bluefruit
switch = digitalio.DigitalInOut(board.D7)

switch.direction = digitalio.Direction.INPUT
switch.pull = digitalio.Pull.UP

# If the switch pin is connected to ground CircuitPython can write to the drive
storage.remount("/", readonly=switch.value)

After you have saved this file to your CIRCUITPY drive, eject CIRCUITPY from your operating system, then press the rest button.

You can find an ‘official’ tutorial for how to use this file here.

Reaction times game

from adafruit_circuitplayground import cp
import time
import random

# Choose the number of data points to collect
N = 5

# Create a list to collect data points
data = [0] * N

# Print some information
print("Welcome to the reaction time game.")
print(f"We will collect {N} samples.")
print("Press button A when an LED lights up.")

# Open file for writing
f = open("/reaction_times.txt","a")
for j in range(N):
    # Turn off all LEDs
    cp.pixels.fill((0, 0, 0))

    # Wait for a random time between 1 and 5 seconds
    random_delay = random.uniform(1, 5)
    time.sleep(random_delay)
    
    # Turn on a random LED (pick an index from 0 to 9)
    led_index = random.randint(0, 9)
    cp.pixels[led_index] = (0, 10, 0)  # Green LED lights up

    # Record the time the LED lights up
    start_time = time.monotonic()

    # Wait for button A press
    while not cp.button_a:
        # do nothing; keep waiting in this while loop
        pass

    # Button pressed! First, calculate the reaction time.
    reaction_time = time.monotonic() - start_time

    # Switch off the LED
    cp.pixels[led_index] = (0, 0, 0)

    # Print the reaction time to the serial console
    print(f"Reaction time: {reaction_time:.3f} seconds")
    
    # Write to file
    f.write(f"{reaction_time:.4f}\n")
    f.flush()
    
    # Pause before restarting the game
    time.sleep(2)

# Close the file for writing.
f.close()

Lec 3.2, Thu Sep 18

Writing your own function

The following is some “starter code” for you to write your own function

from adafruit_circuitplayground import cp
import time
def lightUp(color,n,p):
    # Lights up pixel number n using color "color"
    # 'Color' should be a string, either 'red', 'blue', or 'green'
    # n should be an int between 0 and 9
    # p should be any number between 1 and 255
    return 42

# Now call it inside a while loop
while True:
    lightUp(‘red’,8,45)
    time.sleep(3)
    lightUp('green',5,200)
    time.sleep(3)
    cp.play_tone(440,3)

Lec 4.1, Tue Sep 23

Command Line Programs

import sys

name    = sys.argv[1]
num     = int(sys.argv[2])

print(f"This program prints {name} {num} times.")
for j in range(num):
    print(name)

Save the above code as script1.py. Then, run your code on the command line / terminal by entering:

python3 script1.py testname 5

Lec 4.2, Thu Sep 25

Floating-point IEEE Standard

Lec 5.1, Tue Sep 30

NumPy reference

See the official NumPy documentation here.

Floating Point Error Accumulation

import numpy as np

# Use NumPy's float16 type
a = np.float16(1e-3)  # A small number
n = 10000  # Large number of iterations

result = np.float16(0)  # Start with 0 in float16

# Add the small number 'a' to 'result' n times
for i in range(n):
    result += a

print("Expected result:", a * n)  
print("Result with float16:", result)  # Result with float16

Breaking Floating point numbers

import numpy as np

def showFloat(number):
    # print(f"Binary representation of {number:.3f}, type {type(number)}:")
    if str(type(number)) == "<class 'numpy.float16'>":
        x = np.float16(number)
        bits = x.view(np.uint16)
        return f"{bits:016b}"
    elif str(type(number)) == "<class 'numpy.float32'>":
        x = np.float32(number)
        bits = x.view(np.uint32)
        return f"{bits:032b}"
    elif str(type(number)) == "<class 'numpy.float64'>":
        x = np.float64(number)
        bits = x.view(np.uint64)
        return f"{bits:064b}"
    else:
        print("Type is not compatible")

# Declare some 16-bit floating-point numbers
a = np.float16(128)
c = np.float16(16)
ep = np.float16(0.2)

# Add them together and print them out:

print('128 + 0.2 =',a+ep)
print('128 + 0.2 + 0.2 =',a+ep+ep)
print('128 + 0.2 + 0.2 + 0.2 =',a+ep+ep+ep)
print('128 + (0.2 + 0.2 + 0.2) =',a+(ep+ep+ep))
# View the internals
print(showFloat(a+(ep+ep+ep)))
print(showFloat(a+ep+ep+ep))
print('')

print('16 + 0.2 =',c+ep)
print('16 + 0.2 + 0.2 =',c+ep+ep)
print('16 + 0.2 + 0.2 + 0.2 =',c+ep+ep+ep)
print('16 + (0.2 + 0.2 + 0.2) =',c+(ep+ep+ep))

# View the internals
print(showFloat(c+(ep+ep+ep)))
print(showFloat(c+ep+ep+ep))

Lec 5.2, Thu Oct 2

Basic plotting syntax

import numpy as np
import matplotlib.pyplot as plt


xvals = np.linspace(0,2*np.pi,200)
yvals = np.sin(xvals)

plt.plot(xvals,yvals)
plt.show()

Different plotting styles

# Plot a sine curve
x = np.linspace(0,2*np.pi,20)
y = np.sin(x)

plt.plot(x,y,'o')
plt.show()




# Plot a sine curve
x = np.linspace(0,2*np.pi,15)
y = np.sin(x)

plt.plot(x,y,'o-')
plt.show()

Lec 6.1, Tue Oct 7

Bisection Algorithm

The following code almost implements the bisection algorithm. You must supply the code after the if-statements inside the while loop.

import math
from numpy import sign, cos, pi, exp, sin

def bisection(f,x1,x2,tol):
    # Carries out the bisection algorithm for the function f, using the
    # bracket (x1,x2) with a 'tolerance' of tol.
    f1 = f(x1)
    f2 = f(x2)
    if sign(f1) == sign(f2):
        # if the sign of f(x1) and f(x2) is the same,
        # there is probably no root between x1 and x2.
        print('Root is not bracketed between x1 and x2')
        return None
    
    er = 1 # some large value
    iters = 0
    while er > tol:
        iters+=1
        # uncomment the following line for debugging purposes
        # print(f'Root is between x1 = {x1:.3f} and x2 = {x2:.3f}')
        x3 = 0.5*(x1 + x2)
        f3 = f(x3)
        
        if f3 == 0.0:
            return x3
        if sign(f3) == sign(f2):
            # do something
            # new interval is ...
        else:
            # do something else
            # new interval is ...
            
        er = abs(x1-x2)
    return 0.5*(x1 + x2), iters

# Try it on the function 'cos'
bisection(cos,0.1,3.0,0.001)

Lec 6.2, Thu Oct 9

Lec 8.2, Thu Oct 30

Download the following files in zip format here.

N 6 60 200
Matrix matrix_A_6.csv matrix_A_60.csv matrix_A_200.csv
r.h.s rhs_b_6.csv rhs_b_60.csv rhs_b_200.csv
solution solution_x_6.csv solution_x_60.csv solution_x_200.csv

Numpy’s built-in solver

import numpy as np

A = np.loadtxt('<filename>',delimiter=',')
b = np.loadtxt('<filename>',delimiter=',')

x = np.linalg.solve(A,b)

Conjugate Gradient Algorithm

import numpy as np
from numpy import transpose as tr
from numpy import dot

def conjugate_gradient(A,b,x_guess,tol=1e-6):
    # Uses the conjugate gradient method to solve Ax=b within tolerance specified by 'tol'.
    x = x_guess.copy()
    r = b - dot(A,x)
    beta = 0
    s = r.copy()

    while 2+2 == 4:
        a = dot(tr(s),r)/(dot(dot(tr(s),A),s))  # step size alpha
        x = x + a*s                             # update x
        r = b - dot(A,x)                     # calculate residual
        if norm(r) <  tol:
            break
        beta = - (dot(dot(tr(r),A),s)/
                  (dot(dot(tr(s),A),s)))        # step size beta
        s = r + beta*s                          # update search direction
    return x

Lec 9.2 Thu, Nov 4

Optimize the following function

def shearStress(y):
    return (61224.2 - 1.9334e6*y - 7.01705e8 * y**2 + 4.375e10 * y**3 - 6.81818e11 * y**4)/(0.000686111-0.053333*y+y**2)

Lec 10.1 Tue, Nov 11

1-dimensional optimization

from scipy.optimize import minimize_scalar
import numpy as np
from matplotlib import pyplot as plt

def test_f(x):
    return x**2 - 4*x + 7

solution = minimize_scalar(test_f,[-1,5])

print(f"Function minimized at x = {solution.x:.4f}")

x = np.linspace(-1,5)
plt.plot(x,test_f(x))
plt.grid()
plt.xlabel('y')
plt.ylabel('Shear stress')

plt.scatter(solution.x,test_f(solution.x),marker='o',color='black')
plt.show()

n-dimensional Optimization without constraints

Here, we will minimize the function $f(x,y) = (x-1)^2 + (y+1)^2 + xy$ using scipy’s built-in optimizer.

from scipy.optimize import minimize_scalar,minimize
from numpy.linalg import norm
import numpy as np
import matplotlib.pyplot as plt

def f(xx):
    x = xx[0]
    y = xx[1]
    return (x-1)**2 + (y+1)**2 + x*y

solution = minimize(f,np.array([0.,0.]),method='Powell')

# The rest of the code is just for plotting.
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)

# Calculate the function values over the grid
Z = f([X,Y])

# Create a contour plot
contours = plt.contour(X, Y, Z, levels=20, cmap='viridis')

# Add labels and a color bar
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.colorbar(contours, label='f(x, y)')

# plot the minimum
plt.scatter(solution.x[0],solution.x[1],marker='o',color='black')

# Show the plot
plt.title('Contour Plot of f(x, y)')
plt.show()

n-dimensional optimization with constraints

from scipy.optimize import minimize_scalar,minimize
from numpy.linalg import norm
import numpy as np
import matplotlib.pyplot as plt

# GLOBAL VARIABLE
LAMBDA = 0.01

def f(xx):
    x = xx[0]
    y = xx[1]
    return (x-1)**2 + (y+1)**2 + x*y

def constraint(x,y):
    return (x+1)**2 + (y)**2 - 2

def f_star(x_vector):
    x = x_vector[0]
    y = x_vector[1]
    lam = LAMBDA      # parameter to change
    return f(x_vector) + lam*(constraint(x,y))**2

solution = minimize(f_star,np.array([0.,0.]),method='Powell')

# The rest of the code is just for plotting.
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)

# Calculate the function values over the grid
Z = f([X,Y])

# Create a contour plot
contours = plt.contour(X, Y, Z, levels=20, cmap='viridis')

# plot the constraint
Z_con = constraint(X,Y)
plt.contour(X,Y, Z_con, levels=[0], colors='red', linestyles='solid', linewidths=2)

# Add labels and a color bar
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.grid()
plt.colorbar(contours, label='f(x, y)')

# plot the minimum
plt.scatter(solution.x[0],solution.x[1],marker='o',color='black',label='found minimum')

# Show the plot
plt.title(f'Contour Plot of f(x, y) when lambda = {LAMBDA}')
plt.show()

Powell’s Method from Textbook

This code needs to be modified because I have not provided you with goldSearch.py. You can use scipy’s built-in optimizers instead.

## module powell
''' xMin,nCyc = powell(F,x,h=0.1,tol=1.0e-6)
    Powell's method of minimizing user-supplied function F(x).
    x    = starting point
    h   = initial search increment used in 'bracket'
    xMin = mimimum point
    nCyc = number of cycles
'''
import numpy as np
from goldSearch import *
import math

def powell(F,x,h=0.1,tol=1.0e-6):
    
    def f(s): return F(x + s*v)    # F in direction of v

    n = len(x)                     # Number of design variables
    df = np.zeros(n)               # Decreases of F stored here
    u = np.identity(n)             # Vectors v stored here by rows
    for j in range(30):            # Allow for 30 cycles:
        xOld = x.copy()            # Save starting point
        fOld = F(xOld)
      # First n line searches record decreases of F
        for i in range(n):
            v = u[i]
            a,b = bracket(f,0.0,h)
            s,fMin = search(f,a,b)
            df[i] = fOld - fMin
            fOld = fMin
            x = x + s*v
      # Last line search in the cycle    
        v = x - xOld
        a,b = bracket(f,0.0,h)
        s,fLast = search(f,a,b)
        x = x + s*v
      # Check for convergence
        if math.sqrt(np.dot(x-xOld,x-xOld)/n) < tol: return x,j+1
      # Identify biggest decrease & update search directions
        iMax = np.argmax(df)
        for i in range(iMax,n-1):
            u[i] = u[i+1]
        u[n-1] = v
    print("Powell did not converge")

Lec 10.2 Thu, Nov 13

A function you can test your optimizer on

import numpy as np
from scipy.ndimage import gaussian_filter
from scipy.interpolate import RegularGridInterpolator
import matplotlib.pyplot as plt

def make_noisy_function(n=2, noise_amp=1.0, sigma=10, 
                        xlim=(-10,10), ylim=(-10,10), 
                        resolution=500):
    # This function takes as argument some optional parameters
    # and returns a Python function. So if you run `f = make_noisy_function()`
    # then f will become a function of two variables, i.e., `f(x,y)`.
    # This is an interesting function to minimize. 
    
    # Base grid
    x = np.linspace(*xlim, resolution)
    y = np.linspace(*ylim, resolution)
    X, Y = np.meshgrid(x, y)

    # Base function
    Z = np.sin(n*X) + np.sin(n*Y)

    # Smooth noise
    noise = np.random.randn(*Z.shape)
    smooth_noise = gaussian_filter(noise, sigma=sigma)
    smooth_noise /= np.max(np.abs(smooth_noise))  # normalize to [-1,1]

    # Add noise
    Z_noisy = Z + noise_amp * smooth_noise

    # Interpolator turns it into a callable function f(x, y)
    f_interp = RegularGridInterpolator((x, y), Z_noisy, bounds_error=False, fill_value=None)

    def f(x, y):
        x = np.atleast_1d(x)
        y = np.atleast_1d(y)
        pts = np.column_stack([x, y])
        vals = f_interp(pts)
        if vals.size == 1:
            return vals.item()
        else:
            return vals

    return f

# Use the above constructor to make a function:
f = make_noisy_function(n=2, noise_amp=4.1, sigma=12)

# You may now use the above function in your code.

# Illustrate the function you have just made to visually identify minimia/maxima.

# Create a grid of points
x = np.linspace(-10, 10, 400)
y = np.linspace(-10, 10, 400)
X, Y = np.meshgrid(x, y)

# Evaluate your noisy function over the above grid.
Z = f(X.ravel(), Y.ravel()).reshape(X.shape)

# Plot
plt.figure(figsize=(6,5))
contour = plt.contourf(X, Y, Z, levels=40)
plt.colorbar(contour, label='f(x, y)')
plt.title('Visualize Noisy function')
plt.xlabel('x')
plt.ylabel('y')
plt.tight_layout()
plt.show()

This should produce a function like this:

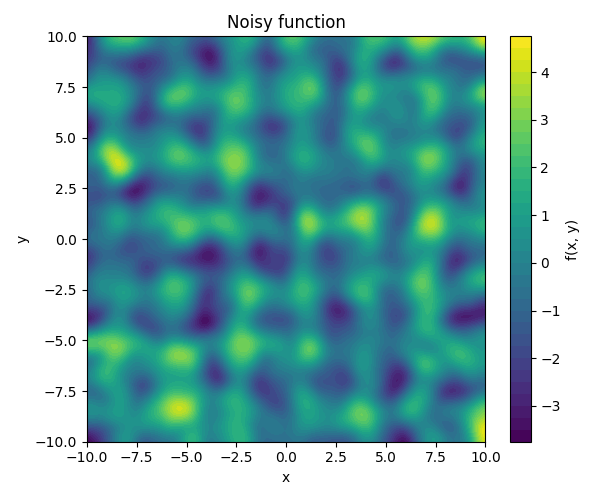
Noisy function

Lec 11.1, Tue, Nov 18

Interpolate these points: download file

Lec 11.2, Thu, Nov 20

Curve-fit these points: download file